Research

The unifying theme of my research is applications of mathematics to music theory and analysis. I have pursued this interest in many different areas of music theory, such as theories of rhythm, harmony, scale theory, musical form, musical structure, and text setting. I am also interested in many different kinds of music, from lesser known composers of 18th century Europe to the 20th-century avant-garde to jazz, Indonesian gamelan, Persian dastgah, and music of the African diaspora.

My book, Organized Time: Rhythm, Tonality, and Form, published by Oxford University Press in 2018, proposes a general framework for temporal structure, which can be applied to rhythmic, tonal, and formal structure. It includes a lot of analysis of classical music from the 18th and 19th centuries, by well-known and lesser known composers. It also shows how we can formulate abstract claims about musical structure and apply mathematical graph theory to them. It won the Society for Music Theory‘s prestigious Wallace Berry Award in 2019. The award committee described it as

. . . a book that is astonishing in both its ambition and its achievement. It offers a theory of tonal music that treats harmony, rhythm, and form as separate dimensions that might either reinforce or contradict each other, providing an appealing notation system that permits direct comparison of these dimensions. It profoundly rethinks aspects of tonal theory that we had thought pretty well settled. The theoretical framework is powerful and the analyses—of both familiar and unfamiliar tonal works—are deeply revealing.

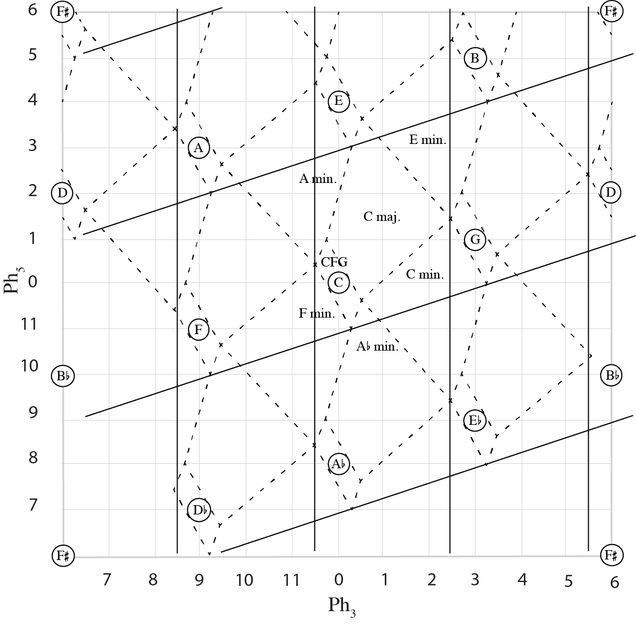
Most of my recent research deals with the two cyclic spaces that govern much of how music works, the temporal cycles of metrical rhythms and grooves, and the pitch cycles of the octave, and an important tool for analyzing objects in these kinds of cyclic spaces, the discrete Fourier transform. A complete list of publications is here. Below are some selected, thematically organized lists.

Forthcoming:

My recent essay, “Tonality and Racism” will be published soon by the Journal of Music Theory along with 10 responses to the essay by leading thinkers in music theory.

Recent: 

I presented “Coherence of Harmonic and Rhythmic Qualities” (powerpoint) at the Mathematical Encounters in Singapore conference on 2/19/2024.

At the joint meeting of the Society and Music Theory and American Musicological Society, Nov. 9–12, 2023, I presented a digital poster with Fabian Moss and Giovanni Affatato, “Animated Harmonic Analysis using DFT Phase Spaces and Coefficient Products,” in which we demonstrated new extensions to the midiverto online music analysis tool.

I did a Zoom colloquium talk for the Society for Music Analysis on Dec. 6, 2023, 18:30 GMT/1:30pm EST entitled “Periodicity and Continuity in Pitch and Time.” Here is the powerpoint (warning: large file!) and a (smaller) pdf.

I presented “Windows into Musical Time” at the Interdisciplinary Approaches to Musical Time conference (Música Analitica, 2nd International Conference),  showing how the paradigm of windowed analysis can lead to a way of understanding the concept of “vertical time.”

I gave a keynote presentation for the Rhythm in Music Since 1900, Sept. 22–24, 2023, on Sat Sept. 23, 11:00–12:15. The title of my talk was “Rhythmic Regularity beyond Meter and Isochrony.” Here is my powerpoint (which is large due to embedded video and audio) and for an easier download, a pdf version.

At the Analytical Approaches to World Music Special Topics Symposium (June 1–8, 2023), I presented on the panel discussion, “Stephen Blum’s Music Theory in Ethnomusicology: A Book Dialogue,” chaired by Michael Tenzer. My comments are here: Music theory nationalized or internationalized: reflections on global music theory occasioned by Stephen Blum’s Music Theory in Ethnomusicology. 

At the meeting of the American Brahms Society, Brahms 2022: New Paths, New Perspectives in New Orleans, Nov. 9–10, I presented on a themed session organized by Richard Cohn, entitled Brahms’s Hybrid Metric Dissonances, 1:30–3:00 on Weds. 11/9. My paper, “Multivalent Displaced Hemiolas in Brahms’s Late Songs” analyzes three songs from Op. 94 and Op. 106 and introduces a visualization of metrical displacement and hemiola I call the “metric cyclone” (slides).

At the Joint Meeting of the American Musicological Society, Society for Music Theory, and Society for Ethnomusicology,  I presented a poster on the SMT poster session from 8–10 AM on Friday Nov. 11. My poster, “Interacting Periodicities in the Music of Ligeti and The Bad Plus” shows how rhythmic spectra can reveal implicit periodicities in “funky” rhythms that can interact, similar in certain ways to polyrhythms, but with a different effect. I draw examples from the later music of modernist composer György Ligeti and the members of the boundary-pushing jazz trio The Bad Plus (Reid Anderson and Dave King) form the early 2000s.

Also at this meeting, I gave a talk for the Mathematics of Music Interest Group of the SMT on Friday, Nov. 11, 12:30–2:00 PM on the mathematical parts of my 2018 book, Organized Time: Rhythm, Tonality, and Form. We will be focusing on Chs. 4, 13, and 14, which introduce properties of structural networks, some graph theory for structural networks, and the idea of the associahedron as a geometry of structural networks.