Open Source
This web site provides open datasets and source code to researchers who desire to contribute to a community of reproducible research. I am happy to share source code & data from papers and projects, as long as appropriate credit is given and it is not being used for commercial purposes. Feel free to email me (leitian AT bu DOT edu) for questions/comments.
For latest updates, check our Github Page.
COMPUTATIONAL IMAGING SYSTEMS & ALGORITHMS
Computational Miniature Mesoscope
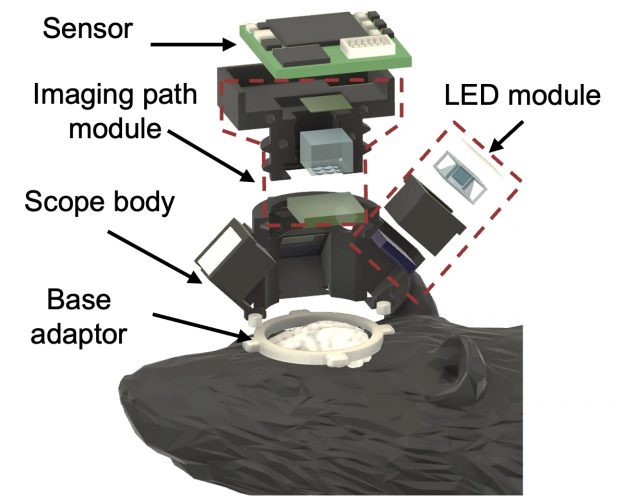 A detail guide on the optical designs and the reconstruction algorithms of Computational Miniature Mesoscope (CM2).
A detail guide on the optical designs and the reconstruction algorithms of Computational Miniature Mesoscope (CM2).
Ref:
Xue, Y., Davison, I. G., Boas, D. A., & Tian, L. (2020). Single-shot 3D wide-field fluorescence imaging with a Computational Miniature Mesoscope. Science advances, 6(43), eabb7508.
Deep learning for biomedical and scientific imaging
Dynamic Synthesis Network for adaptive 3D descattering
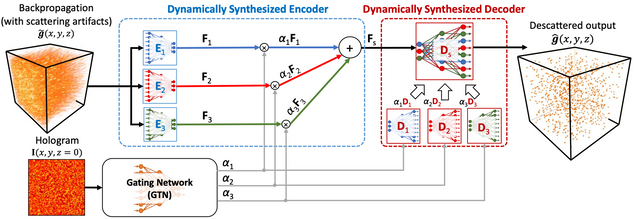
The implementation of the dynamic synthesis network (DSN) for large-scale 3D descattering, as presented in our publication:
W. Tahir, H. Wang, L. Tian, “Adaptive 3D descattering with a dynamic synthesis network“, Light: Science & Applications volume 11, Article number: 42 (2022).
Self-supervised Learning for Voltage Imaging Denoising
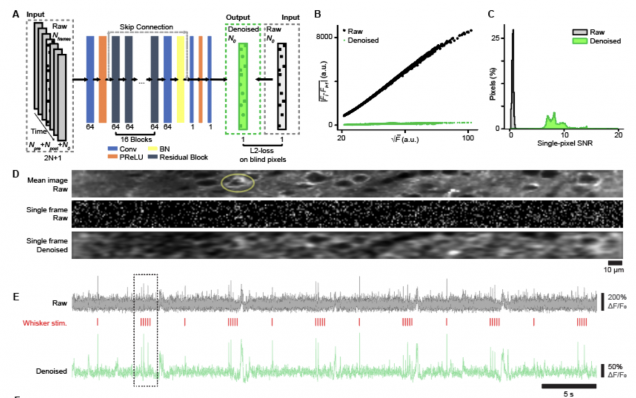
The implementation of the self-supervised denoising deep learning model (DeepVID) for two-photon voltage imaging data , as presented in the publication:
Platisa, J., Ye, X., Ahrens, A. M., Liu, C., Chen, I. A., Davison, I. G., … & Chen, J. L. (2021). High-Speed Low-Light In Vivo Two-Photon Voltage Imaging of Large Neuronal Populations. bioRxiv.
Uncertainty quantification using Bayesian neural network for coded illumination phase imaging
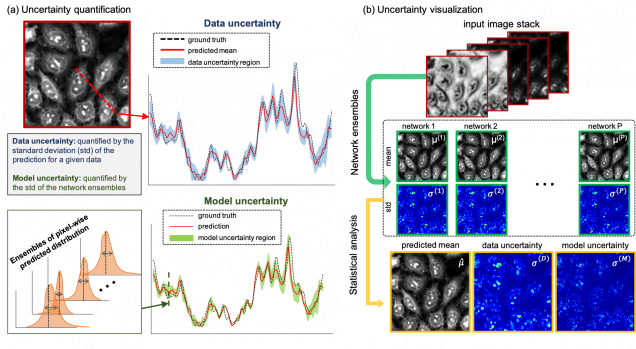
Python (TensorFlow+Keras) implementation of the Bayesian convolutional neural network to enable uncertainty learning and solving the inverse problem of recovering high-resolution phase from five multiplexed intensity measurements.
Reference:
Deep speckle correlation
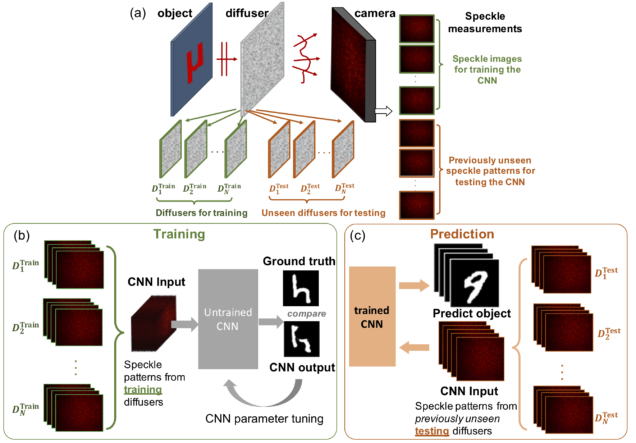
Python (TensorFlow+Keras) implementation of the convolutional neural network to enable “one-to-all” mapping of speckles generated by a whole class of diffusers. This allows one to perform training on a sub-set of diffusers while imaging through an entirely different set of “unseen” diffusers.
Reference:
2PM Vascular Segmentation DNN
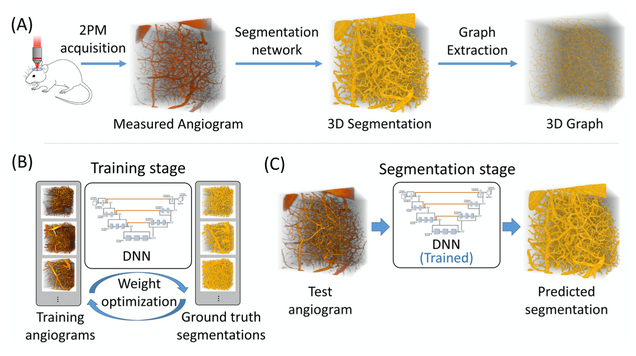
Our deep learning framework with a loss function that incorporates a balanced binary-cross-entropy loss and a total variation regularization on the network’s output. Its effectiveness has been demonstrated on experimentally acquired in-vivo angiograms from mouse brains of dimensions up to 808×808×702 μm.
Reference:
Multiple scattering simulation and computational imaging
Holographic Particle 3D Imaging with BPM
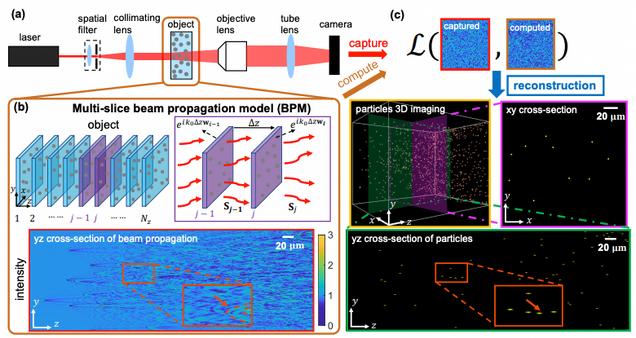
Matlab implementation of our BPM model based forward model and reconstruction algorithm for holographic particle field imaging.
Reference:
Wang, Hao, et al. “Large-scale holographic particle 3D imaging with the beam propagation model. arXiv:2103.05808 (2021).
Statistical Beam propagation method (sBPM)
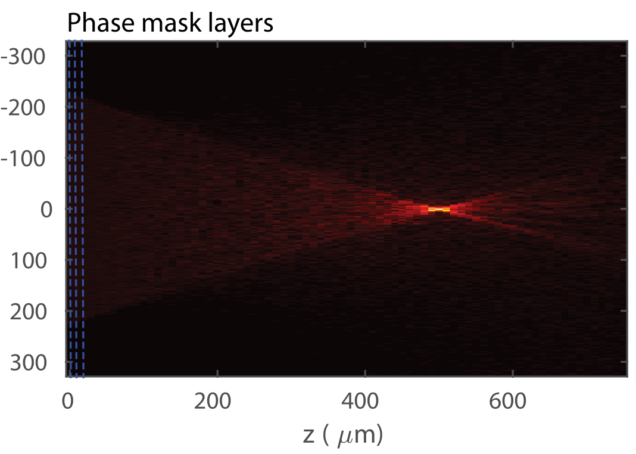
Matlab implementation of our statistical BPM model that calculates the wavefront propagation in a scattering medium with the scattering mean free path (ls) and anisotropy factor (g) characterized.
Reference:
Intensity Diffraction Tomography
Split-step non-paraxial model for intensity diffraction tomography
Repository for SSNP-IDT: Split-step non-paraxial model based IDT reconstruction that works for both sequential and multiplexed measurements. Implementation in Python.
High-speed in vitro intensity diffraction tomography using Annular Illumination (aIDT)
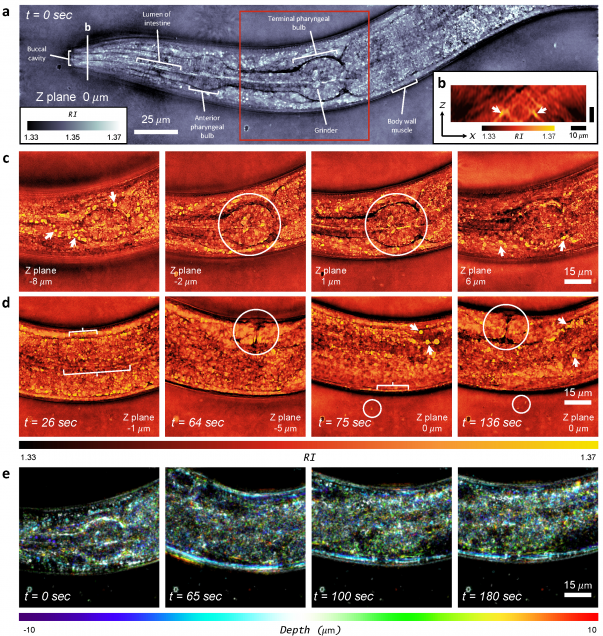
MATLAB implementation of intensity diffraction tomography using annular illumination to enable high speed characterization of large-volume 3D refractive index distributions in vitro.
Slice-wise IDT phase and amplitude reconstruction using Tikhonov regularization
MATLAB implementation of slice-wise intensity diffraction tomography reconstruction of complex permittivity distribution based on 1st Born approximation. Example data included that were taken on an LED array microscope.
Reference:
Reflection intensity phase microscopy
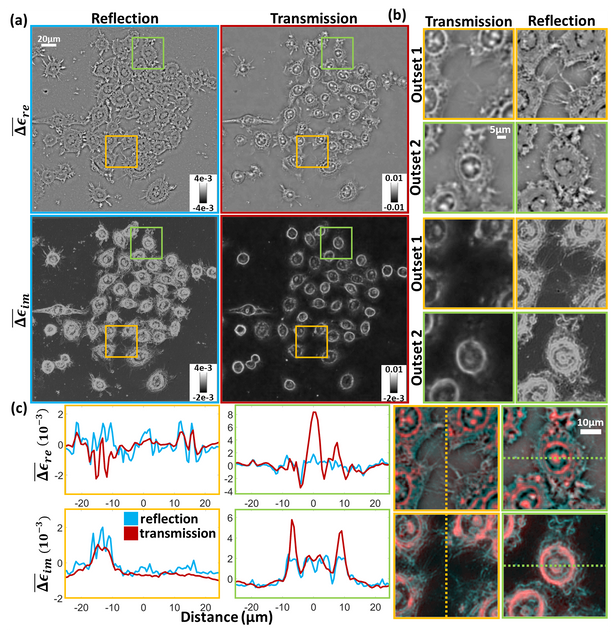
MATLAB implementation of the reflection intensity phase microscopy reconstruction pipeline.
Reference:
Alex Matlock, Anne Sentenac, Patrick C. Chaumet, Ji Yi, and Lei Tian, “Inverse scattering for reflection intensity phase microscopy,” Biomed. Opt. Express 11, 911-926 (2020).
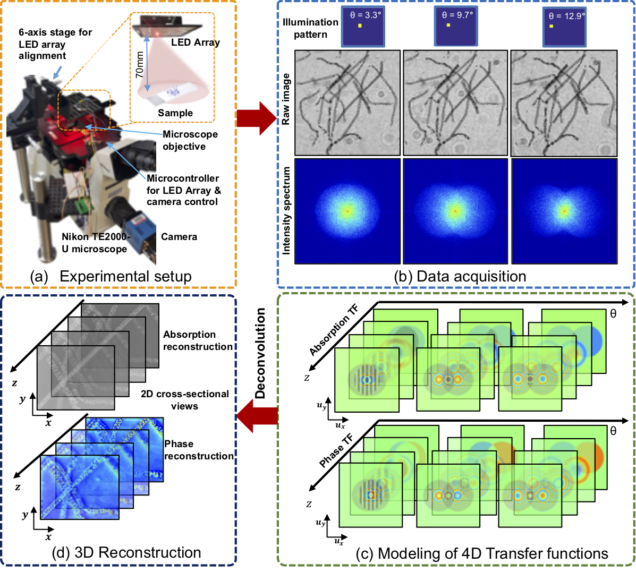
Computational Microscopy with Coded Illumination
Fourier ptychography reconstruction algorithm with Quasi-Newton’s method
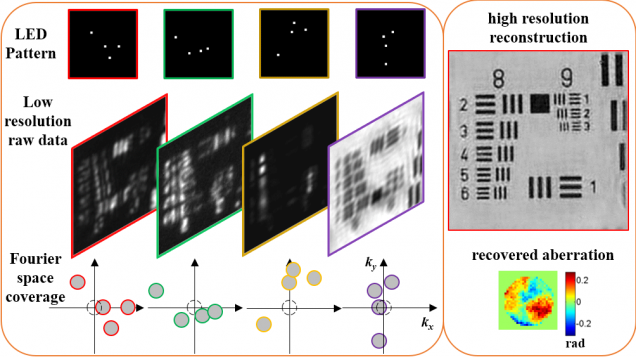
Matlab code implements Fourier ptychography reconstruction algorithm from a set of images captured under different illumination angles (e.g. in an LED array microscope), using either sequential or multiplexed coded illumination. The algorithm simultaneously estimates the complex object function (amplitude + phase) with high resolution (defined by objective NA+illumination NA) and the pupil function (aberrations). It implements a sequential quasi-Newton’s method with Tikhonov (L2) regularization.
Reference:
L. Tian, X. Li, K. Ramchandran, and L. Waller, “Multiplexed coded illumination for Fourier Ptychography with an LED array microscope,” Biomedical Optics Express 5, 2376-2389 (2014).
3D Fourier ptychography on LED array microscope
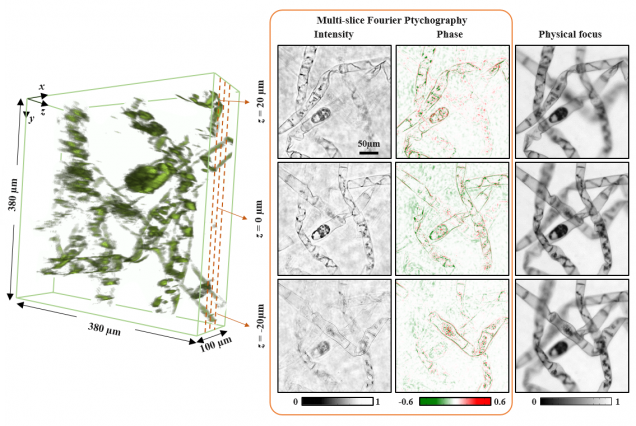
Matlab code contains images captured from sequential LED illumination up to 0.41 NA, using a 4x objective (0.1 NA). In our paper, we achieved resolution corresponding to the sum of the two NAs~0.5. Our 3D FPM algorithms is based on multislice model that accounts for multiple scattering effects from 3D model. It combines 3D light field refocusing with FPM to achieve super resolution in both lateral (x,y) and axial (z) dimensions across a large field of view.
Reference:
Lei Tian, Laura Waller, 3D intensity and phase imaging from light field measurements in an LED array microscope, Optica 2, 104-111 (2015).
Quantitative DPC phase imaging on LED array microscope

Matlab code implements a Tikhonov deconvolution based phase reconstruction algorithm from single or multi-axis DPC data. Images should be captured with LED array illumination using two complementary asymmetric patterns (e.g. halves of the brightfield circle) on in each image. The transfer functions are calculated according to the Weak Object Transfer Function and solve for phase in the least squares sense. The complementary images are subtracted and DPC images contain the phase gradient information.
Reference:
Lei Tian, Laura Waller, Quantitative differential phase contrast imaging in an LED array microscope, Opt. Express 23, 11394-11403 (2015).
Light field refocusing and 3D differential phase contrast (DPC) on LED array microscope
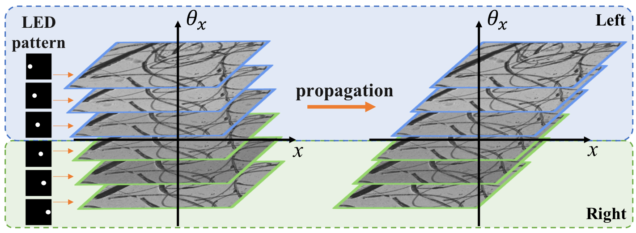
Matlab code implements the popular ‘shift-and-add’ light field digital refocusing algorithm. The code is designed for processing data captured by sequentially turning on an array of illumination angles on our LED array microscope. It then splits the data based on illumination angles according to the differential phase contrast (DPC) method to compute the phase gradient information of the sample. The same algorithms can be also used for lenslet-based light field microscope.
Reference:
Lei Tian, et al., 3D differential phase contrast microscopy with computational illumination using an LED array, Opt. Lett. 9, 1326 – 1329 (2014).
Phase Imaging from Defocus
Compressive phase tomography based on Transport of Intensity Equation (TIE)
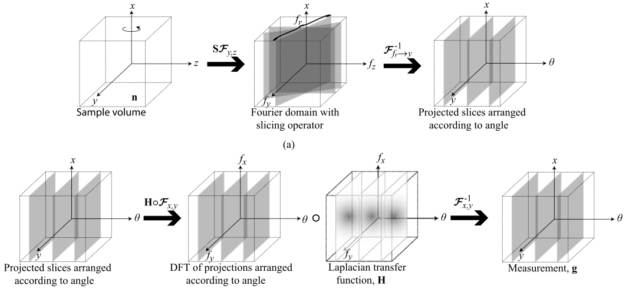
Matlab code implements a 3D total variation (TV) based compressive reconstruction algorithm for tomographic recovery of 3D refractive index distribution for weakly attenuating objects from angularly sparsely measured data. Our model makes the projection approximation which works well for X-ray phase tomography. The operator adapts the non-uniform FFT (NUFFT) to account for radial Fourier sampling in tomography. The 3D TV-minimization is implemented by a modified TwIST algorithm.
Reference:
Lei Tian, et al., Compressive X-ray phase tomography based on the transport of intensity equation, Opt. Lett. 38, 3418-3421 (2013).
Digital Holography
Simulation of holograms from particle clouds based on Mie scattering theory

Matlab code simulates in-line (Gabor) holograms from 3D distributions of dielectric particles. The code makes the 1st Born approximation, which only accounts for single scatterings from particles but not higher order wave optic interactions. The total scattered field is calculated as the linear sum from the scattered fields from each particles. The Mie scattering calculation is adapted from the work of Christian Maetzler.
Reference:
Lei Tian, Chapter 2 of my thesis “Compressive phase retrieval“, MIT 2013.
W. Chen, et. al, Empirical concentration bounds for compressive holographic bubble imaging based on a Mie scattering model, Opt. Express 23, 4715-4725 (2015)
DATASETS
Computational Microscopy with Coded Illumination
Fourier ptychographic microscopy (FPM) on LED array microscope
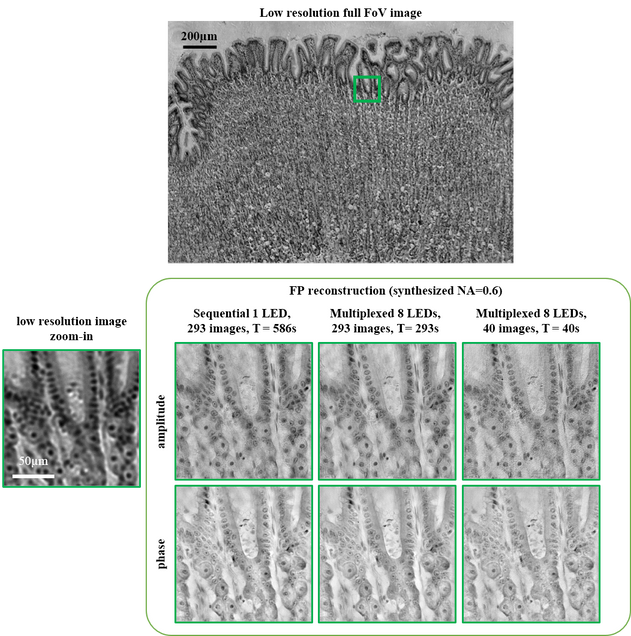
Dataset contains images captured from two different LED patterning methods (sequential and randomly multiplexed) within 0.5 illumination NA, from a 4x objective. In our paper, we achieved resolution corresponding to the sum of the two NAs~0.6, using a new FPM algorithms based on alternating projection with a modified Newton’s method. The setup uses an LED array (e.g. Adafruit) placed at ~60 – 70mm above the sample on a Nikon TE300 microscope. Details on experiments are listed in a separate text file included.
Dataset 1: stained histology slide, our reconstruction is here
Dataset 2: USAF resolution target
FAQs:
- If you have trouble in reading in the images in the proper order (1,2,3, …) , try this Natural-Order Filename Sort.
Reference:
Lei Tian, et al., Multiplexed coded illumination for Fourier Ptychography with an LED array microscope, Biomed. Opt. Express 5, 2376-2389 (2014).
Quantitative Phase Imaging using FPM on LED array microscope
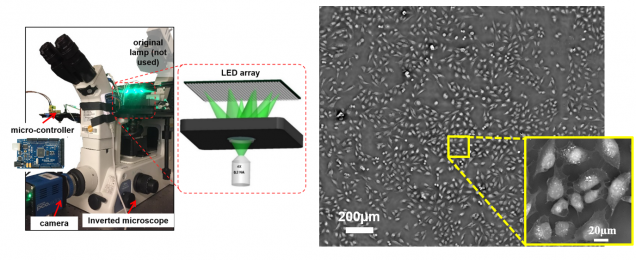
FPM also enables label-free quantitative phase imaging capability. Datasets contain images captured from unstained fixed and live cell cultures.
Dataset 1: in vitro Hela cell culture
Dataset 2: fixed stained and unstained U2OS cell sample, our reconstruction is here
Reference:
Lei Tian, et al. Computational illumination for high-speed in vitro Fourier ptychographic microscopy, Optica 2, 904-911 (2015).