A DFT Analysis of Raman Signatures of Pt-Au Interactions in Quasi-One Dimensional Metal-Organic Nanowires

Vivian Pazmany ’18, B.S. in Electrical Engineering with a concentration in Nanotechnology.
Metallophilic interactions between closed shell metal ions with electron configurations, d8, d9 and d10, are widely studied, because these interactions are essential to the behavior of molecular conductors in molecular electronics. Metal-metal interactions occur between atoms with single valence electrons, where the valence and conduction bands of both metals, in this research, Pt+ and Au-, might express an overlap in energetic bands. When closely packed into a crystal structure, atoms’ valence electrons will overlap causing electrons to delocalize forming a free electron system. A conductive material will have an overlap in energy bands and electron delocalization. Therefore, Pt+ and Au-, when close in proximity, have closed-shell interactions that makes them effective as conductors, similar to the weak effects of Van der Waals interactions.
We can understand these interactions using vibrational spectra. Raman spectroscopy uses photons to shift the crystal into a temporary state of excitation. If there is an overlap in energetic bands, meaning metal-metal interactions between the metallic core atoms and their valence electrons, this state of temporary excitement will exhibit a noticeable attraction between the two metallic cores. Therefore, Raman spectroscopy is an effective tool to measure metallophilic interactions.
This research studies the vibrational properties of tunable quasi-one-dimensional metal- organic chains that are promising as electronic and spintronic materials. These structures consist of single chains of the form [Pt(tpy)X][AuY2] that self-assemble as weakly bound wires within an anisotropic crystal in the solid-state, forming salts of alternating Pt+ and Au- atoms embedded in organic matrices [Hayoun, R.; Zhong, D. K.; Rheingold, A. L.; Doerrer, L. H. Inorganic Chem., 2006, 45(16), 6120-6122]. Here, we utilize density functional theory (DFT) and Raman spectroscopy (as implemented in Gaussian 09 and Quantum Espresso) in order to probe their structural and vibrational properties. By comparison of prediction with measurements, we determine the optical signatures of intra-chain, specifically the Au… Pt mode found experimentally at 140cm-1, and inter-chain interactions of the quasi-one dimensional crystals.
We used calculated frequency spectra of 6 different clusters, where results with and without periodic boundary conditions were compared to experiment. Our simulations do not contain the packing forces of infinite neighboring chains which would exist experimentally. Therefore, geometry optimization caused the metallic cores to expand from 3.349Å to 4.067Å, a distance too large for metal-metal contacts to form; thus, we used experimental geometry. The different clusters allowed us to identify vibrational modes of intra-chain, inter-chain and anion-cation interactions within the wires. The single chain clusters allowed us to identify the modes corresponding to intra-chain and anion-cation interactions, while the double chain clusters allowed us to identify inter-chain interactions and effects that neighboring chains might have on the vibrational spectra.
We first calculated the Raman spectra of our single chain two aperiodic-units cluster and double chain two aperiodic-units cluster using Gaussian 09. B3LYP was used to calculate the Raman spectra of the single chain two aperiodic-units cluster. B3LYP with dispersion correction (IOp(3/124=3) was used to calculate the Raman spectra of the double chain two aperiodic-units cluster in order to include Van der Waals forces.
We proceeded to calculate the vibrational spectra of both clusters with periodic boundary conditions. Parameters used in Quantum Espresso were as follows: LDA functional and norm- conserving pseudopotentials in separable (Kleinman-Bylander) form, gamma-only, free structure with specified cell parameters. Atomic coordinates were the same as the experimental coordinates used in the structures of the aperiodic calculations, for consistency. Dispersion correction was included as Grimme-D2 scheme. Generally, total energy convergence can be achieved with a rather low wave function cutoff of 120Ry; however, we found that the calculated spectra varied greatly from 120Ry to 300Ry. Due to computational limitations, we were not able to compute vibrational modes with a wave function cutoff higher than 300Ry. Feasible total energy convergence studies allowed us to choose a suitable wave-function cutoff (300 Ry) and k- point density (9x5x3). Similar to the aperiodic calculations, we did not optimize the geometry and instead opted for experimental geometry.
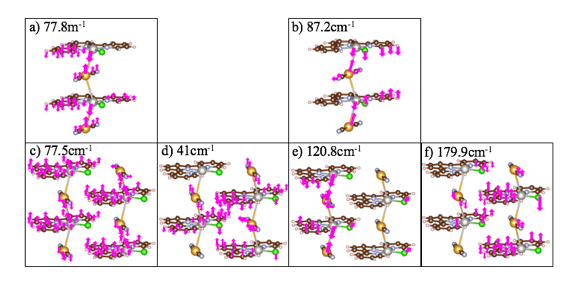
The Raman cation-anion mode for the aperiodic single chain cluster is observed at a) 77.8cm-1 and the same mode is observed at b) 87.2cm-1, for the single chain periodic cluster. The Raman cation-anion and inter-chain modes for the double chain aperiodic cluster are found at c) 77.5cm-1 and at d) 41cm-1 respectively. The Raman modes for cation-anion and inter-chain interactions for the double chain periodic cluster are found at e) 120.8cm-1 and f) 179.9cm-1 respectively.
We calculated inter-chain interactions for the double chain two aperiodic-units clusters and double chain two periodic-units cluster at 41cm-1 and 179.9 cm-1 respectively. The cation-anion modes for the single chain two aperiodic-units cluster, single chain two periodic-units cluster, and double chain two aperiodic-units cluster, were found at 77.8 cm-1, 87.2 cm-1 and 77.5 cm-1 respectively. As for the double chain two periodic-units cluster, theoretical results found intra-chain modes for cation-anion interactions in the range, 115-148 cm-1, similar to the experimental peak, 140 cm-1. Furthermore, the terpyridine peaks in the range, 700-1650 cm-1, are blue shifted for the theoretical spectrum compared to the experimental, which is also why we observe cation-anion interactions in a slightly lower range as well. These results are consistent and a promising start to confirming metallophilic interactions and ultimately, conductivity.
In conclusion, the double chain two-periodic units cluster yielded the most accurate results for Raman vibrational modes of the [Pt(tpy)Cl]+…[Au(CN)2]- self-assembled nanowires compared to experiment. This is to be expected, because it is most closely related to experiment environment in terms of neighboring chains and periodicity. The aperiodic calculations and single chain two periodic-units calculations produced cation-anion modes much lower than experiment, 140 cm-1. To produce the most accurate DTF calculations, it is necessary to calculate the spectra of the bulk structure, or even a cluster with 4-plus adjacent chains; for, periodic boundary conditions had a substantial effect on the vibrational spectra.
