Dimensionality reduction for neural data analysis
My name is Munib Hasnain and I am a first year PhD Student in the Biomedical Engineering Department at Boston University. I rotated in the Chand Lab during April and May 2020 where I learned about and applied dimensionality reduction techniques to neural data.
Advances in recording techniques have enabled neuroscientists to record activity from large populations of neurons simultaneously. This has enabled researchers to formulate population-level hypotheses and has opened up the sorts of analyses that can be performed. One form of analysis is dimensionality reduction, in which we seek low-dimensional representations of high-dimensional data – the idea being that there may be shared activity or mechanisms among a population of neurons that can describe the entire population. Dimensionality reduction methods extract these explanatory or latent variables and discard unexplained variance as noise. There are many methods to perform dimensionality reduction, but not all are suitable for neural data. During my rotation, I applied four different methods to understand their applicability to neural data and to get a sense of what it takes to implement them.
The first method I looked at was Principal Component Analysis (PCA). PCA seeks to find the direction of maximal variance in a dataset. All principal components are orthogonal to each other and are simply the eigenvectors of the data covariance matrix. Dimensionality reduction is achieved by projecting the original data onto some number of the principal components found through PCA. Although PCA is a powerful technique, it is generally only applied to trial-averaged data as it does not have a noise component. The lack of a noise model hinders the technique’s ability to capture the true dynamics of the neural population, since neurons may contain both shared and independent variance.
Factor Analysis (FA), on the other hand, can be thought of as similar to PCA, but contains an implicit noise model that is capable of separating the shared variance of neurons from the independent variance, thus making it more suitable to single-trial data analysis. The goal of applying PCA and FA are exactly the same, but FA has been explicitly designed to identify latent variables, whereas PCA provides an approximation to those latent variables.
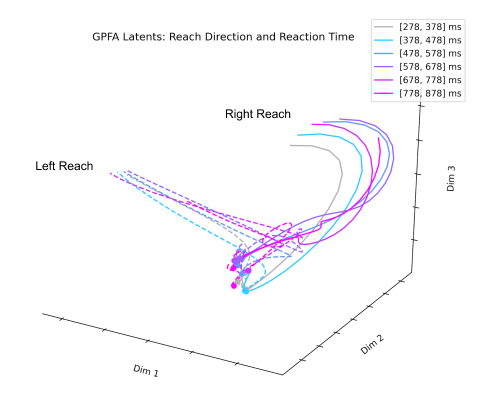
The next technique I looked at was Gaussian Process Factor Analysis (GPFA). When applying PCA or FA to neural data, the data must be smoothed over time before dimensionality reduction. GPFA combines both smoothing and dimensionality reduction into a unified process in order to ensure that both the degree of smoothness and the relationship between latent and original activity are optimized together. GPFA has been applied extensively to neural data and seems to be one of the more popular techniques for extracting latent neural trajectories.
Lastly, I looked at Variational Latent Gaussian Processes (vLGP). This technique is similar to GPFA in that smoothing and dimensionality reduction are combined into a single process. vLPG differs from GPFA in that it assumes neural spiking to be follow a point process, which can be seen as preserving information between firing rate bins that may be lost in techniques such as GPFA. Both GPFA and vLGP are suitable for single-trial neural data analysis.
My time in the Chand Lab was extremely valuable and I hope to be able to continue learning and applying large-scale neural data techniques to answer interesting questions about behavior and motor control. If you are interested in seeing the implementation of these techniques to both simulated and real data, you can find my code on GitHub.