The space of essential matrices as a Riemannian manifold

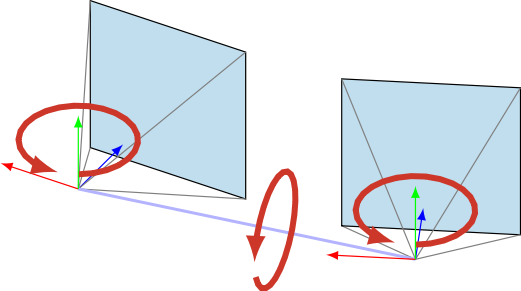
The images of 3-D points in two views are related by the so-called _essential matrix_.
There have been attempts to characterize the space of valid essential matrices as a Riemannian manifold. These approaches either put an unnatural emphasis on one of the two cameras, or do not accurately take into account the geometric meaning of the representation.

We addressed these limitations[^1] by proposing a new parametrization which aligns the global reference frame with the baseline between the two cameras. This provides a symmetric, geometrically meaningful representation which can be naturally derived as a quotient manifold. This not only provides a principled way to define distances between essential matrices, but it also sheds new light on older results (such as the well-known twisted pair ambiguity).

We provide an implementation of the basic function for working with the essential manifold integrated with the Matlab toolbox MANOPT. Download link: Manopt 1.06b with essential manifold.