Intelligent Active Sensing and Temporal Logic in Belief Space
Active sensing is the problem of coordinating a robot or team of robot’s motion and sensor alignment such that they can estimate some spacially distributed feature of the environment. An example of such a problem is a team of aerial robots with onboard cameras being used to monitor traffic conditions in an urban environment. The robots should give preference to visiting busy intersections that are likely to be congested, those areas of the city that have not recently been observed, and places where the images they previously recorded were ambiguous
Many algorithms based on information theory have been successfully developed to address various active sensing scenarios. However, many of the tasks that these procedures are constructed to accomplish are much simpler than the scenarios that robots acting in complex, dynamic environments would encounter. Consider the following illustration.
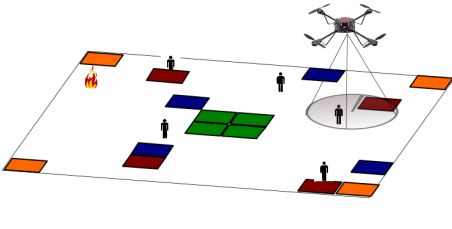
In this scenario, the aerial robot is tasked with locating human survivors and potential fires in an urban area immediately after a natural disaster, such as an earthquake. If a survivor is found in an unsafe region (denoted by red), then the robot must guide the humans to a safe pickup region (green) before reporting its location at a data upload hub (blue). If the survivor is in a safe region or a fire is found, then the robot needs to report its location at a data upload region. Once the robot has localized survivors as well as possible, it must exit the scene (orange regions).
In order to complete this task, the robot must plan its motion on-line such that it gathers information about some spatial feature (survivor locations), reacts to gains in information (report locations of survivors when they are found) and organize tasks sequentially (ensure survivor safety before reporting locations). While state-of-the-art active sensing algorithms deal very well with information gathering, they are not easily extended to the other planning tasks.
In order to integrate reactive and sequential planning into active sensing, we turn to the field of temporal logic planning. Temporal logics (TLs) are extensions of Boolean logic that integrate how the state of a system may evolve over time . An example of a task that may be described by a TL formula is “Visit Region A and then Region B while always avoiding hazards. If Region C is entered, go to region D before entering region B. ” Such rich missions cannot be decomposed into simple “go from point A to point B” specifications We combine TLs with active sensing in the following two ways.
Temporal Logic-Constrained Informative Path Planning
We first consider applications in which the temporal logic mission is given over known features of the environment, e.g. the robot is operating in an environment with known topology and has to avoid hazards while visiting a sequence of regions. The robot is also tasked with forming a minimal uncertainty (minimal Shannon entropy) measure of some a priori unknown feature, a problem known as the informative path planning problem.
Preliminary results may be found here. We have developed a way to combine TL and informative planning into a single mathematical framework and developed two algorithms, an off-line expectation maximization and an on-line receding horizon procedure, to solve this problem. We have developed stochastic dynamic programming versions of these algorithms. Currently, we are validating these results on experimental platforms. Future research directions include extending our results to multi-agent systems.
Distribution Temporal Logic
Next, we consider applications in which the temporal logic mission is given over unknown features of the environment, e.g. in the above example, the robot must find the survivor and guide it to a safe location. In order to address this type of problem, we have developed a novel paradigm called distribution temporal logic (DTL) which can be used to describe such tasks. DTL is a temporal logic defined over sample paths of random processes (e.g. the unknown underlying state of the environment) and functions of estimate distributions (e.g. measures of uncertainty or expected costs). DTL can be used to express such missions as “Explore the environment until the entropy of the estimate of the survivor locations is below 5 bits. If a survivor is found in an unsafe location with probability 0.8, guide it to a safe region.” DTL is defined in full here. Our current research focuses on developing algorithms to find control policies that maximize the probability of satisfying a given DTL specification.

