Atmospheric turbulence

The atmospheric boundary layer, which spans from the Earth’s surface to about 1-2 kms above the ground, is highly turbulent (i.e., full of random and swirling motions). Understanding turbulent transport of momentum and scalars such as water vapor and CO2 in the atmospheric boundary layer plays an important role in many disciplines such as meteorology, hydrology, agriculture and air quality control. One particularly interesting feature of atmospheric turbulence is that it is not only generated by shear force but also affected by buoyancy force (sometimes also called stability) resulting from surface heating and cooling in a typical diurnal cycle.

As a result of buoyancy, many turbulent theories need to be adjusted and many assumptions applicable to neutral conditions (i.e., there is no buoyancy) break down. For example, it is often assumed that turbulence transports momentum and scalars similarly, which is usually referred to as the Reynolds analogy. This has been demonstrated to be incorrect under unstable conditions in our work using experimental data and phenomenological models such as Figure 1(Li and Bou-Zeid, 2011; Li et al. 2012).

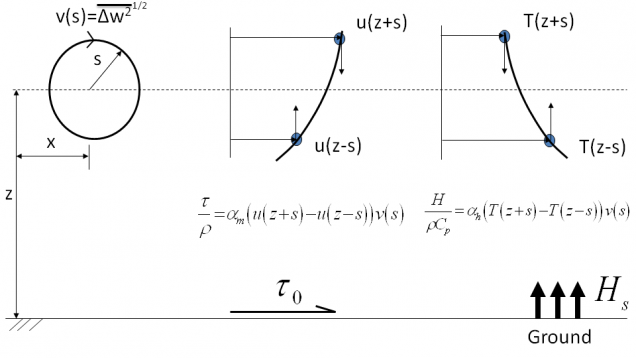Figure 1: Turbulent momentum and sensible heat fluxes due to the turnover of an isotropic eddy of radius s acting on a mean velocity and temperature profile.

In addition, it is also often assumed that turbulence transports all scalars similarly. This assumption has been implicitly used in numerous applications including most numerical weather and climate models. The dissimilarity between active scalars (i.e., scalars that affect the flow dynamics such as sensible heat) and passive scalars (i.e., scalars that hardly affect the flow dynamics such as water vapor and CO2) is another important topic studied in our group (Li et al. 2012; Zhao et al. 2013; Wang et al. 2014; Sun et al. 2015). For example, we used the dissimilarity measure between water vapor and temperature to parameterize the Priestley-Taylor coefficient over water surfaces (Assouline et al. 2016).

Monin-Obukhov similarity theory, proposed more than 60 years ago, remains the basic framework for us to understand the impact of buoyancy on turbulent characteristics in the atmospheric surface layer. How we can tackle Monin-Obukhov similarity functions from a theoretical perspective remains elusive. In a series of work inspired by recently-proposed linkages between turbulent spectra and mean velocity profile in pipe flows, we theoretically derived mean velocity/temperature profiles based on idealized turbulent spectra of velocity velocity and air temperature as shown in Figure 2 (Katul et al. 2013; Li et al. 2015a ; Li et al. 2015b). The model is also applied to understand the turbulent longitudinal velocity variance (Banerjee et al. 2015) and the ‘-1’ scaling in the temperature spectrum (Li et al. 2016).

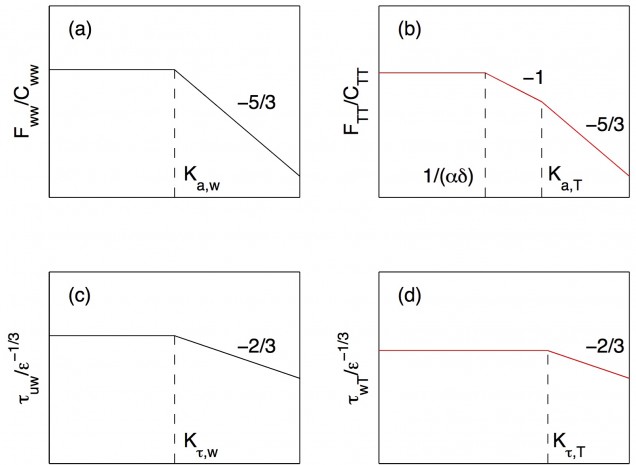
Figure 2: The idealized spectra of vertical velocity (a), air temperature (b), eddy turnover scale for momentum flux (c) and heat flux (d).

In summary, turbulent transport is one of the most important processes in the atmospheric boundary layer and has important implications. Our aim is to better understand turbulent transport under idealized and non-idealized conditions, which forms the basis to design better parameterizations that can be utilized in numerical models.