Research projects
My research interests lie at the intersection of automatic control, robotics and computer vision. I am particularly interested in applications of Riemannian geometry and in distributed problems involving teams of multiple agents.
Unified Vision-Based Motion Estimation and Control for Multiple and Complex Robots
Overview
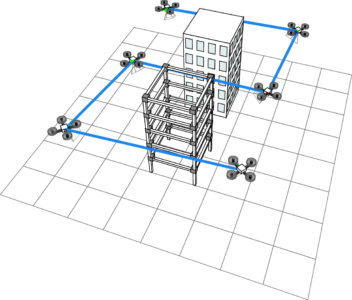
The project considers teams of robots that need to collaborate on a physical task. As a driving application, we consider a Robot Construction Crew that needs to assemble a building using prefabricated components. Each robot might have non-trivial kinematics (e.g., a robotic arm mounted on a non-holonomic platform), and is generally equipped with vision sensors (cameras). To achieve their mission, the robots need to:
- Localize themselves with respect to each other, to the construction area, and to the prefabricated components that need to be assembled.
- Coordinate their motions to collaboratively grasp, transport and assemble the components
- Plan how to survey and inspect the results of their work.


We introduce novel optimization formulations that take advantage of this structure by combining the vision-kinodynamic constraints into convex constraints (e.g., defining a Semi-Definite Program) and non-convex low-rank constraints (from the bilinearity over translations and rotations). We expect that this methodology will surpass current state- of-the-art solutions, by providing robust joint solvers instead of cumbersome and brittle pipelines.
Funding and support
 This project is supported by the National Science Foundation grant "Unified Vision-Based Motion Estimation and Control for Multiple and Complex Robots" (Award number 2212051)
This project is supported by the National Science Foundation grant "Unified Vision-Based Motion Estimation and Control for Multiple and Complex Robots" (Award number 2212051)
Start date: August 1, 2022
End date: July 31, 2025
Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Multimodal, Task-Aware Movement Quality Assessment and Control: From the Clinic to the Home
Overview
The goal of the project is to develop a novel, distributed sensor platform that continuously assesses movement in the background of one’s life and facilitates personalized, ”smart” intervention when detecting movement dysfunctions and functional decline, with the goal of helping people age in place and avoid expensive and lengthy hospitalizations.
Motivation
Frail older adults constitute the sickest, most expensive, and fastest growing segment of the US population. However, the US health care system fails on most counts to promptly detect and act on the loss of function and the onset of frailty. It instead reacts to catastrophic events with intensive, high-cost, hospital- and institution-based interventions. Home-based technologies that enable timely diagnosis of the functional decline and movement dysfunctions that are known to precipitate the onset of frailty are desperately needed to facilitate aging in place. Moreover, next-generation powered assistive technologies are emerging as promising tools for both assistance and rehabilitation. Current solutions, however, are limited to specific actions (walking) in controlled conditions, and depend on body-worn sensors that provide limited context for control. These limitations render unconstrained use of these devices in free-living settings as a distant vision.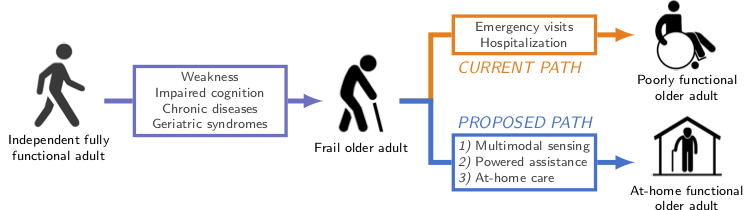
Aims
-
- Develop a multimodal sensor platform that fuses data and recognizes basic actions from body-worn sensors and external cameras.
- Test the platform in a clinical setting to enable activity- and context-aware motion assessment and control across a range of walking-related activities (e.g., sit-to-stand, walking, turning, stairs).
- Test the platform in home-based deployments to enable caregiver alerts in response to detected functional decline.
Funding and support
 This project is supported by the National Institute of Health/National Institute on Aging grant "SCH: Multimodal,Task-Aware Movement Assessment and Control: Clinic to Home".
This project is supported by the National Institute of Health/National Institute on Aging grant "SCH: Multimodal,Task-Aware Movement Assessment and Control: Clinic to Home".
Start date: September 30th, 2010
End date: May 31st, 2023
Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of NIH or the U.S. Government.
Distributed semantic processing in camera networks
Overview
In many applications, sensor networks can be used to monitor large geographical regions. This typically produces large quantities of data that need to be associated, summarized and classified in order to arrive to a semantically meaningful descriptions of the phenomena being monitored. The long-term guiding vision of this project is a distributed network that can perform this analysis autonomously, over long periods of times, and in a scalable way. As a concrete application, this research focuses on smart camera networks with nodes that are either static or part of robotic agents. The planned work will result in systems that are more efficient, accurate, and resilient. The algorithms developed will find wide applications, including in security (continuously detecting suspicious individuals in real time) and the Internet of Things. As part of the broader impacts, the project will produce educational material to explain the scientific results of the project to a K12 audience.
QuickMatch: Fast Multi-Image Matching via Density-Based Clustering
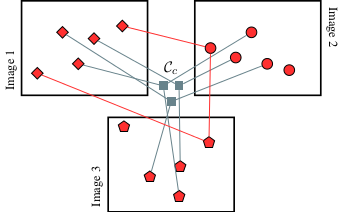
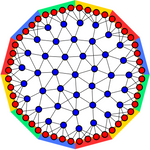
The first result of this project is an algorithm, QuickMatch, that performs consistent matching across multiple images. Quickmatch formulates the problem as a clustering problem (see figure) and then uses a modified density-based algorithm to separate the points in clusters that represents consistent matches across images.
In particular, with respect to previous work, QuickMatch 1) represents a novel application of density-based clustering; 2) directly outputs consistent multi-image matches without explicit pre-processing (e.g., initial pairwise decisions) or post-processing (e.g., thresholding of a matrix); 3) is non-iterative, deterministic, and initialization-free; 4) produces better results in a small fraction of the time (it is up to 62 times faster in some benchmarks); 5) can scale to large datasets that previous methods cannot handle (it has been tested with more than 20k+ features); 6) takes advantage of the distinctiveness of the descriptor as done in traditional matching to counteract the problem of repeated structures; 7) does not assume a one-to-one correspondence of features between images; 8) does not need a-priori knowledge of the number of entities (i.e., clusters) present in the images. Code is available under the Software page.
NetMatch (Distributed QuickMatch)
NetMatch (a.k.a. Distributed QuickMatch) is a distributed version of QuickMatch, our density-clustering-based algorithm for multi-image matching. The primary extensions introduced by NetMatch are:
- We introduce a method for distributing the matching problem across multiple agents based on a feature space partition.
- We introduce a lightweight method to resolve conflict arising from clusters straddling different elements of the feature space partition.
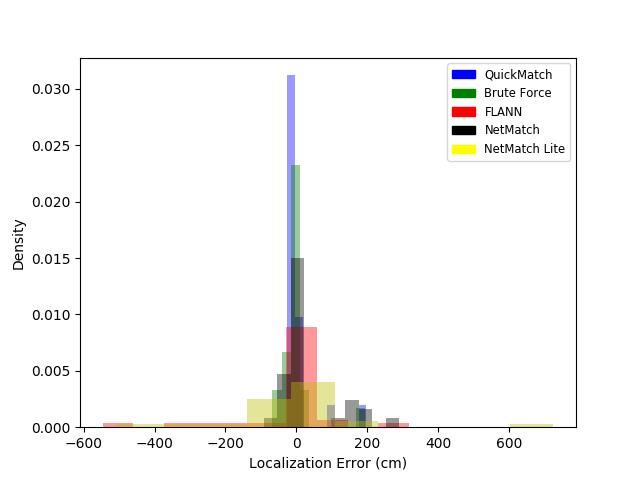
- We demonstrate the distributed solution is nearly equivalent to the centralized feature matching solution, and minimizes inter-agent communication
Overall, NetMatch extends the QuickMatch framework to handle distributed computation with minimal loss to match quality, and minimal inter-agent communication, at the expense of additional computations due to the need of determining, for each data point, whether it might be part of a cluster split over different elements of the partition.
A preliminary implementation of NetMatch Lite based on the Robotic Operating System (ROS) is available on a git repository (https://github.com/JackJin96/Distributed_Numbers_ROS).
"NetMatch: the Game", an educational board game
We developed an alpha version of a board game, called NetMatch, that provides a tangible and fun way to explain the main research challenges in the project. This game is for two to four players, whose goal is to move their pawns across a network (one hop at a time) from the edges in order to match pawns with similar symbols. When all the pawns for a symbol are matched, a letter for a secret word is revealed. The player that discovers all the letters of his word is the winner.
To start playing, simply download, print, and cut the pieces from the PDF document.
The majority of the game's components components (board, cards, pawns) are procedurally generated. The code is made freely available, so that it is possible to easily generate variations of the game. The code made available on a git repository (https://bitbucket.org/tronroberto/pythonnetmatchgame).
If you play the game, please complete the four-questions feedback form at https://forms.gle/zpKurzJuTJwxWqts7.
Personnel information
| Tron, Roberto | PI |
| Karimian, Arman | Graduate Student |
| Berlind, Carter | Undergraduate Student |
| Sookraj, Brandon | Undergraduate Student |
| Jin, Hanchong | Undergraduate Student |
Publications and other resources
You can also follow the journey of two of the undergraduate students involved on the project on their respective blogs:
| Sookraj, Brandon | https://sookrajrobotics.wordpress.com |
| Jin, Hanchong | https://2020hjfm.weebly.com/blogs |
Funding and support
 This project is supported by the National Science Foundation grant "III: Small: Distributed Semantic Information Processing Applied to Camera Sensor Networks" (Award number 1717656).
This project is supported by the National Science Foundation grant "III: Small: Distributed Semantic Information Processing Applied to Camera Sensor Networks" (Award number 1717656).
Start date: September 1, 2017
End date: August 31, 2020
Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Robust, Scalable, Distributed Semantic Mapping for Search-and-Rescue and Manufacturing Co-Robots
Overview
The goal of this project is to enable multiple co-robots to map and understand the environment they are in to efficiently collaborate among themselves and with human operators in education, medical assistance, agriculture, and manufacturing applications. The first distinctive characteristic of this project is that the environment will be modeled semantically, that is, it will contain human-interpretable labels (e.g., object category names) in addition to geometric data. This will be achieved through a novel, robust integration of methods from both computer vision and robotics, allowing easier communications between robots and humans in the field. The second distinctive characteristic of this project is that the increased computation load due to the addition of human-interpretable information will be handled by judiciously approximating and spreading the computations across the entire network. The novel developed methods will be evaluated by emulating real-world scenarios in manufacturing and for search-and-rescue operations, leading to potential benefits for large segments of the society. The project will include opportunities for training students at the high-school, undergraduate, and graduate levels by promoting the development of marketable skills.
This is a joint project with Dario Pompili at Rutgers University.
Rotational Outlier Identification in Pose Graphs using Dual Decomposition
The first result of this project is an outlier detection algorithm that finds
incorrect relative poses in pose graphs by checking the geometric consistency of
their cycles. This is an essential step in mapping
unknown environments with single or multiple robots, as incorrectly estimated
relative poses lead to failure in mapping techniques such as
Structure from Motion (SfM) or Simultaneous Localization and Mapping (SLAM).
Increasing the robustness of this process is an active research area, as
incorrect measurements are unavoidable due to feature mismatch or repetitive
structures in the environment.
Our algorithm provides: 1) a novel probabilistic framework for detecting outliers
from the rotational component of relative poses, which uses the geometric
consistency of cycles in the pose graph as evidence; 2) a novel inference algorithm,
of independent interest, which utilizes dual decomposition to break the inference
problem into smaller sub-problems which can be solved in parallel and in a
distributed fashion; 3) an Expectation-Maximization scheme to fine-tune the
distribution parameters and prior information iteratively.
Publications
Software
We therefore developed pySLAM-D, a new SLAM pipeline that addresses two gaps in existing SLAM packages (such as ORB SLAM):
- The main implementation is in Python and has a very modular architecture. This allows faster development and implementation of research ideas, such as the integration with modern learning frameworks such as TensorFlow and PyTorch.
- It incorporates recent advancements in individual modules (such as the TEASER algorithm for point cloud alignment)
For further details see: pySLAM-D: an open-source library for localization and mapping with depth cameras.
SLAM Dataset
We have collected a new RGB-D SLAM dataset in the BU Robotics Lab. The full dataset can be downloaded at the following link:
The BU Robotics Lab SLAM dataset
Personnel information (BU)
| Tron, Roberto | PI |
| Serlin, Zachary | Graduate Student |
| Yang, Guang | Graduate Student |
| Sookraj, Brandon | Research Experience for Undergraduates (REU) Participant |
| Jin, Hanchong | Research Experience for Undergraduates (REU) Participant |
| Wallace, Gordon | Undergraduate Student |
| Zhu, Jialin | Undergraduate Student |
| Gerontis, Constantinos | Undergraduate Student |
| Pietraski, Miranda | High School Student |
Funding and support
This project is supported by the National Science Foundation grant "Robust, Scalable, Distributed Semantic Mapping for Search-and-Rescue and Manufacturing Co-Robots" (Award number 1734454).

Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Control of Micro Aerial Vehicles under Aerodynamic and Physical Contact Interactions
Overview
The goal of this project is to make quadrotors and other similar small-scale flying rotorcraft safer and easier to fly. Both recreational and commercial use of these vehicles has recently surged in popularity. However, safety concerns about potentially damaging collisions limit their deployment near people or in close formation, and the current state of the art in vehicle control is insufficient for potential applications involving flight inside of complicated structures such as industrial plants, forests and caves. This project will lead to innovations in control schemes, aerodynamic interactions modeling, and robust aerial vehicles design. Together, these innovations will make small-scale vehicles less likely to cause unintended damage, suitable for use in extreme environments such as caves, and more easily piloted. This will allow in turn the use of these vehicles in new industrial monitoring and search-and-rescue applications, thus bringing the benefits of these platforms to larger segments of society.
Contraction theory and Riemannian tangent bundles
We started by considering attitude-only controllers; in this case, the state space can be modeled as the tangent bundle of the Special Orthogonal Lie group (i.e., as the space of rotations together with their angular velocities). Building upon previous work, the metric and the differentiation operator that are used in standard contraction theory for Euclidean spaces correspond, respectively to the Riemannian metric and covariant differentiation on Riemannian manifolds, and the differentiation operation corresponds to covariant differentiation. However, existing results for covariant differentiation on tangent bundles (which is what is required for our application) can be applied only to a specific type of metric (the Sasaki metric, which is only a particular case of natural metrics). The first step under this grant, therefore, has been to generalize existing results to a more general class of non-natural metrics. While previous natural metrics, intuitively, do not allow "interaction" between changes in rotations and changes in velocity, our new class of metrics instead explicitly allows such "interactions".
Improved geometric control
Building upon the results above, we have applied the generalized metric for the bundle to the actual problem of geometric attitude control for quadrotors. The key in this application is that the contraction metric is a linear matrix inequality with a special structure stemming from the configuration manifold, allowing for an efficient search of metric coefficients and tuning of the controller coefficients that prove exponential stability of the controller. The work on our Riemannian contraction control framework resulted in a geometric attitude controller that is locally exponentially stable and almost globally asymptotically stable; the exponential convergence region is much larger than existing non-hybrid geometric controllers (and covers almost the entire rotation space). As an additional contribution, we proposed a general framework to automatically select controller gains by optimizing bounds on the system’s convergence rate; while this principle is quite general, its application is particularly straightforward in the case of our contraction-based controller.
Using designed reference trajectories for improved convergence
We extended the almost-globally exponentially stable controller described above to include a reference trajectory that exponentially converges to the ultimate desired equilibrium. This extension our approach truly globally exponentially convergent for the rotation component, although discontinuous in terms of the initial conditions. From a technical standpoint, this requires extendeding our approach from using a bundle metric (on the tangent bundle TSO(3)) to product manifolds (TSO(3) times SO(3)); this required finding new ways to bound the cross-terms that arise in the contraction condition. We also changed the automatic parameter tuning procedure from a grid search to a derivative-free optimization search, due to the increase in the number of parameters in the contraction condition. Of note is that the convergence rate of the reference trajectory (which is a design parameter) is optimized along those of the Riemannian metric.
Aerodynamic simulation of small-scale quadrotors
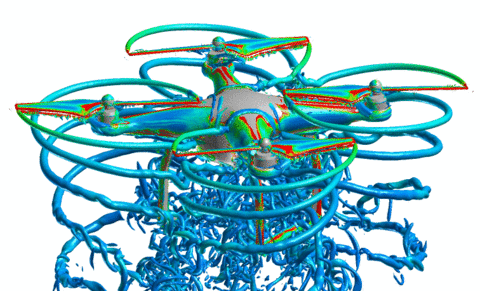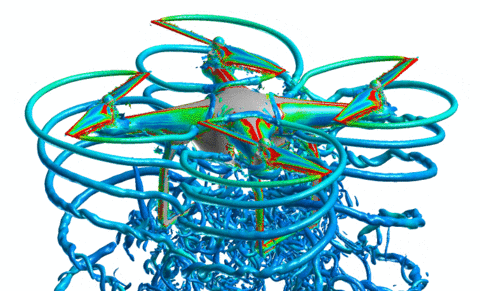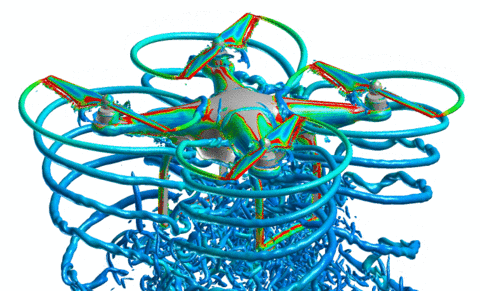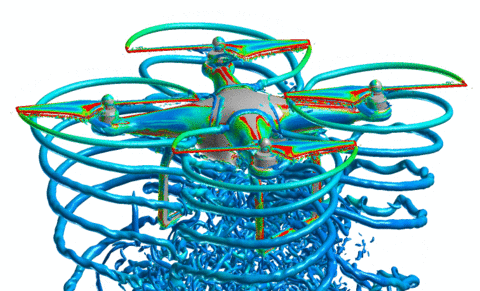
We begun simulations of small quadrotors in order to fully develop the computational capability to characterize the aerodynamics associated with these systems. The student has been trained to use the Helios softward suite of codes originally developed for analyzing helicopter aerodynamics. The effect of near-body CFD base method and turbulence model choice as well as transition model on the simulation results have been study in order to determine a best computational method. The Spalart Allmaras model with no transition method was shown to work well to predict thrust. This method was then used to analyze flow effects found in multirotor systems including rotor-fuselage interactions and fountain flow (which leads to flow reingestion). A computational study of the influence of these phenomena based on rotor placement has been started. The development of the computational capability will enable further investigation and understanding, together with the experiments, of the behavior of important aerodynamic parameters that are used in the control algorithms such as the coefficient of thrust and the blade-flap angle. Most recently, the PhD student has worked with the developers of the Helios suite to include a method for modeling RPM-based trim. This capability will allow us to now move from characterization of hover performance to maneuvering performance. Initial results of our aerodynamic simulations show that when the rotors are close to the fuselage the competing forces from the ground effect and the reingestion lead to a nonlinear thrust relation with angular velocity for the rotors. In addition, there is a nonlinear download on the fuselage. All of these aerodynamic effects are nonlinear functions of the distance of the rotor from the fuselage. It does seem that there is an optimal placement where best performance is achieved, but further investigation is needed to fully specify such a configuration.
Experimental aerodynamic characterization of quadrotors

One of the objectives of the project is to develop low-order models that better capture the aerodynamic effects in the system due to its geometry, operating conditions, and presence of nearby surfaces. These models will be developed by a combined use of experimental data and detailed simulations. In this regard, we have developed an experimental platform for collecting and characterizing the relation between commands given to the rotors in an aerial vehicle (quadrotor), and the actual forces and torques generated. The setup involves an industrial-grade 6-D force-torque sensor, and a custom quadrotor platform (based on the PixHawk microcontroller).
Smart cage

One of the objectives of the project is to develop a suspended smart cage that not only protects the quadrotor, but also functions as a sensor during contacts (measuring forces and displacements).
We have currently completed a physical prototype of the smart cage (see picture on the right). In addition, he also developed related algorithms for obtaining the pose of the outer cage rim with respect to the body-fixed base (based on solutions of polynomial equations and iterative refinements), and the location of the vehicle in a known map (based on particle filtering) from the potentiometers embedded in the platform.
Publications
Personnel information
| Tron, Roberto | PI |
| Grace, Sheryl | Co-PO |
| Vang, Bee | Graduate Student |
| Thai, Austin | Graduate Student |
| Liu, Cheng | Master Student |
| Dudek, Kurt | Research Experience for Undergraduates (REU) Participant |
| Hafling, Justin | Research Experience for Undergraduates (REU) Participant |
| Amy Pinto - Quintanilla | Research Experience for Undergraduates (REU) Participant |
| Costiner, Smaranda | High School Student |
Funding and support
 This project is supported by the National Science Foundation grant "Control of Micro Aerial Vehicles under Aerodynamic and Physical Contact Interactions" (Award number 1728277).
This project is supported by the National Science Foundation grant "Control of Micro Aerial Vehicles under Aerodynamic and Physical Contact Interactions" (Award number 1728277).
Start date: September 1, 2017
End date: August 31, 2022
Disclaimer: Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation.
Vision-based formation control
The goal of formation control is to move a group of agents in order to achieve and maintain a set of desired relative positions. This problem has a long history, and latest trends emphasize the use of vision-based solution. In this setting, the measurement of the relative direction (i.e., bearing) between two agents can be quite accurate, while the measurement of their distance is typically less reliable.
We propose a general solution which is based on pure bearing measurements, optionally augmented with the corresponding distances. As opposed to the state of the art, our control law does not require auxiliary distance measurements or estimators, it can be applied to leaderless or leader-based formations with arbitrary topologies. Our framework is based on distributed optimization, and it has global convergence guarantees.
We have experimentally validated our approach on a platform of three quadrotors.

The space of essential matrices as a Riemannian manifold
The images of 3-D points in two views are related by the so-called _essential matrix_.
There have been attempts to characterize the space of valid essential matrices as a Riemannian manifold. These approaches either put an unnatural emphasis on one of the two cameras, or do not accurately take into account the geometric meaning of the representation.
We addressed these limitations[^1] by proposing a new parametrization which aligns the global reference frame with the baseline between the two cameras. This provides a symmetric, geometrically meaningful representation which can be naturally derived as a quotient manifold. This not only provides a principled way to define distances between essential matrices, but it also sheds new light on older results (such as the well-known twisted pair ambiguity).
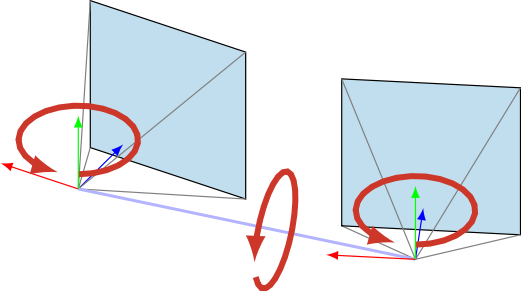
We provide an implementation of the basic function for working with the essential manifold integrated with the Matlab toolbox MANOPT. Download link: Manopt 1.06b with essential manifold.
Distributed localization algorithms
Imagine a wireless camera network, where each camera has a piece of local information, e.g., the pose of the object from a specific viewpoint or the relative poses with respect to the neighboring cameras.
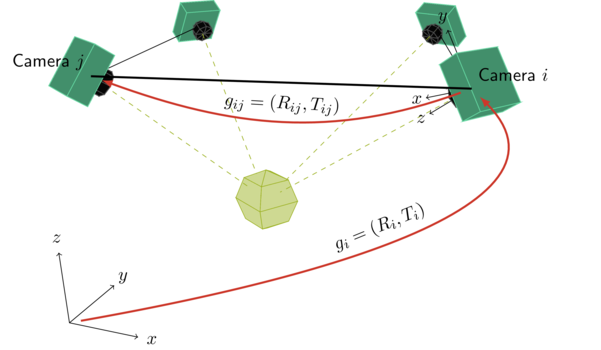
It is natural to look for distributed algorithms which merge all these local measurements into a single, globally consistent estimate. I derived such algorithms by formulating a global optimization problem over the space of poses, and shown their convergence from a large set of initial conditions using the aforementioned theoretical tools.
Consensus algorithms on Riemannian manifolds
Given a group of agents which move in Euclidean space and communicate according to a given communication graph, standard consensus algorithms provide a protocol which, as time passes, brings all the agents to a common location. The key aspect here is that only local communications are used. These algorithms, however, do not apply when the agents evolve on a manifold (for instance, imagine a group of satellites synchronizing their poses). Using my theoretical work, I proposed a natural extension for this case, and characterized its convergence for a large class of manifolds.
This work was awarded Best Student Paper and Best Student Paper Runner-up at the IEEE Conference for Decision and Control (CDC) in 2012 and 2011, respectively.
Distributed optimization on Riemannian manifolds
I worked on distributed optimization problems involving variables lying on non-linear spaces (that is, Riemannian manifolds) using extensions of gradient descent algorithms with fixed step size. I developed novel theoretical tools which significantly broadened the state of the art for determining sufficient conditions for global behaviors (algorithm convergence) using only local information. These tools have been used in consensus algorithms, camera localization and formation control.