Coordinated Agile Control of Aerial Vehicles

This project studies agile maneuvering of unmanned aerial vehicles, particularly for quadcopters. Our methods incorporate differential flatness theory, which simplifies path planning and control for the quadcopter’s nonlinear dynamics.

Topic 1:
Aggressive maneuvering by trajectory generation. From differential flatness theory, a feasible trajectory can be designed for the aircraft by specifying the position and the yaw angle. Knowing the initial and final position, velocity, acceleration, jerk and snap, and also the travel time between them, a dynamically feasible trajectory can be generated in the 12-dimensional state space of quadrotor. Two examples are shown below.

Agile maneuvering with precise landing:

Dancing with aggressive trajecotries:

 

Topic 2:
Using differential flatness to enable precise vector field following. We use differential flatness to design feedback controllers to guide the aircraft through a desired 2D or 3D vector field, as shown in the Figure below.  Our method compensates for the complex internal dynamics of the quadrotor allowing it to follow the vector field precisely, even in vector fields that require agile maneuvering.

One application of the vector field is for obstacle avoidance, in the field that the obstacle has a repulse vector field in its vicinity and the destination of the quadcopter has a attracting vector field, so that the quadcopter would fly to the destination without colliding into the obstacle.

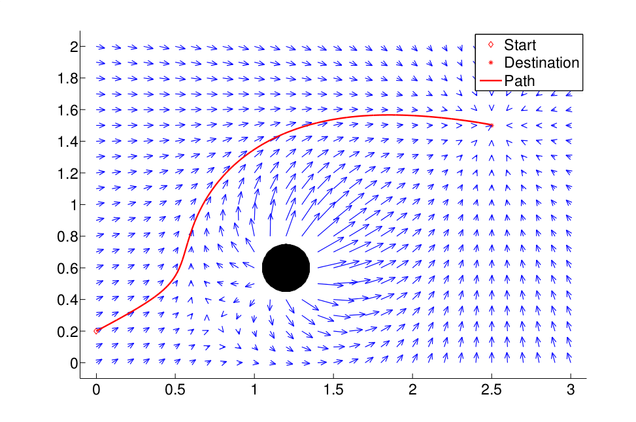
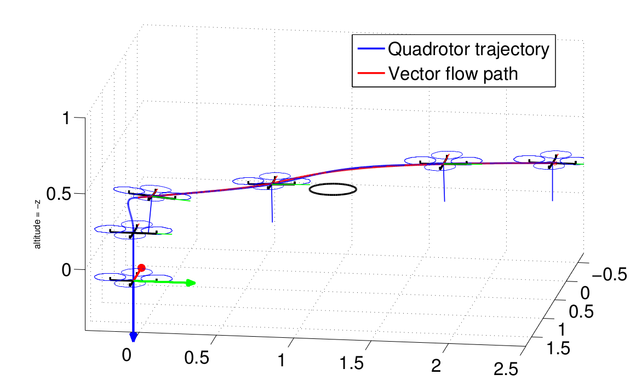
Notice that the virtual obstacle in the field is not plotted.

 

Topic 3:
Autonomous flight of a team of quadcopters, based on our new abstraction called Virtual Rigid Body (VRB). With VRB, we can simply treat the group of quadcopters as a single rigid body, that we will be able to plan its trajectory in the kinematic regime. But inside the framework of VRB, we can plan the trajectories of the quadrotors to transit (we call it a transformation) from one formation to another, with collision avoidance be guaranteed. A simulation and then an experiment video with three KMel K500 quadrotors is shown as below.

 

Topic 4:
Followed from topic 3, in which the trajectory of the VRB is planned before hand, we developed more algorithms that are able to fly a VRB, or a team of quadcopters, from a standard gaming joystick (Logitech Extreme 3D pro) manually. We also created a suitable motion primitive library, so that the transformation is not needed to be planned in real time. The below video shows a flight with five KMel Nano Plus quadrotors. The transformations are triggered from joystick buttons.